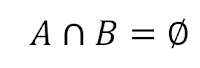Bloque 1
Eje: Manejo de la información
Tema: Nociones de probabilidad
Aprendizajes esperados: Explicar la diferencia entre eventos complementarios, mutuamente excluyentes e independientes.
DEFINICIÓN DE PROBABILIDAD
La probabilidad es la posibilidad de que ocurra un determinado suceso.
ESCALA DE PROBABILIDAD
La posibilidad de que ocurra un evento se mide con una escala. Esta escala es del 0 al 1, ente más cerca al 0 es poco probable y entre más cerca del 1 es muy probable que ocurra.
Un
experimento aleatorio es aquel del que no podemos predecir su resultado al practicarse, por ejemplo:
Lanzar un dado
Girar una ruleta
Girar una perinola
Jugar a la lotería
Un
evento es, por ejemplo:
Evento A: "Que caiga el número 6 al lanza un dado"
Para conocer la probabilidad de que suceda este evento, necesito conocer ciertos datos:
ESPACIO MUESTRAL.- Todos los posibles resultados
Al lanzar un dado, todos los posibles resultados son 1, 2, 3, 4, 5 y 6
se escribe E={1, 2, 3, 4, 5, 6}
PROBABILIDAD.- Calcular la posibilidad de ocurrencia de un evento o suceso. Se escribe P(A)
y se calcula de la siguiente manera.
EVENTO COMPLEMENTARIO
Son dos resultados de un evento, siendo éstos los dos únicos resultados posibles.
Ejemplo 1
Cuando lanzas una moneda, las dos opciones son águila o sol, como no hay más opciones, estos eventos son complementarios.
Evento A: "Caiga Sol"
Evento B: "Caiga Aguila"
Evento A es complementario de Evento B
Ejemplo 2
Cuando lanzas un dado y que salga 1 o 2 no es complementario, ya que hay otros resultados posibles (2, 3, 4, 5, 6)
Pero lanzar un dado y obtener 1 o algo diferente a 1 son eventos complementarios.
Evento A: "Salga 1"
Evento B: "No salga 1"
Evento A es complementario de Evento B
EVENTO MUTUAMENTE EXCLUYENTE
Son dos resultados de un evento que no pueden ocurrir al mismo tiempo.
Ejemplo 1
Al lanzar una moneda, puede salir sol o puede salir águila, no hay otra opción.
Evento A: "Salga sol"
Evento B: "Salga águila"
Como son mutuamente excluyentes, la probabilidad de que
A o B suceda se escribe así:
P(AUB) =
para encontrar la probabilidad se tienen que sumar las probabilidades del suceso A y del suceso B.
P(AUB) = P(A) + P(B)
EJERCICIOS
1)
EXPERIMENTO: Lanzar un dado
Espacio Muestral E={1,2,3,4,5,6}
Evento A: "Cae un número primo menor a 3" (El 1 no es primo, entonces sólo el 2)
A={2}
Evento B:"Cae un número igual o mayor a 3"
B={3,4,5,6}
La
intersección de estos eventos se escribe
y se lee: "A intersección B es igual al vacío" que significa que no hay elementos de A que estén en B, por lo que deducimos que no podrían ocurrir al mismo tiempo los dos eventos y entonces son MUTUAMENTE EXCLUYENTES.
La
unión de estos eventos se escribe
y se lee: "A unión B es igual a los elementos 2, 3, 4, 5 y 6" que significa que se unieron los elementos de A={2} y de B={3,4,5,6}
2)
EXPERIMENTO: Lanzar un dado
Espacio Muestral E={1,2,3,4,5,6}
Evento A: "Cae un número menor a 3"
A={1, 2}
Evento B:"Cae un número igual o mayor a 3"
B={3,4,5,6}
La
intersección de estos eventos se escribe
y se lee: "A intersección B es igual al vacío" que significa que no hay elementos de A que estén en B, por lo que deducimos que no podrían ocurrir al mismo tiempo los dos eventos y entonces son MUTUAMENTE EXCLUYENTES.
La
unión de estos eventos se escribe
y se lee: "A unión B es igual a los elementos 1, 2, 3, 4, 5 y 6" que significa que se unieron los elementos de A={1, 2} y de B={3,4,5,6}
Si observas, la unión de A y B es la misma que el espacio muestral por lo que a estos eventos se les llama COMPLEMENTARIOS
INDICACIONES
1) Descarga e imprime
2) Resuelve con lápiz
3) Entrega en la fecha indicada
DESCARGAR PDF